Em vez de retas, círculos e esferas, esta geometria usa fractais e atratores estranhos para modelar a natureza.
Neste artigo, exploraremos o fascinante mundo dos fractais, um ramo da matemática que desvenda os segredos da geometria da natureza. Fractais, concebidos pelo renomado Benoît Mandelbrot, revelam padrões ocultos nas aparentes irregularidades do nosso ambiente natural, oferecendo insights profundos que vão desde a compreensão de formas complexas até aplicações práticas em campos tão diversos quanto engenharia, medicina e ciência da computação. Ao adentrarmos nesse universo intrigante, descobriremos como os fractais transcenderam a matemática pura para se tornarem uma ferramenta essencial na compreensão do nosso mundo.

Inspirado pelo livro “Almanaque das Curiosidades Matemáticas”, de Ian Stewart, convidamos você a adentrar no emocionante mundo dos fractais. Aqui, exploraremos a intrigante geometria da natureza, revelando os segredos matemáticos por trás das formas complexas e aparentemente caóticas que povoam nosso ambiente natural.
Desenvolvidos por Benoît Mandelbrot e introduzidos ao mundo em 1975, os fractais não são apenas um campo da matemática, mas também uma poderosa ferramenta que revolucionou nossa compreensão da complexidade intrínseca à realidade que nos cerca.
Descubra como essas estruturas intrincadas têm aplicações que abrangem desde a otimização de antenas de telefonia celular até a detecção de células cancerosas, navegando por diversas áreas da ciência e da tecnologia.
Este artigo é uma jornada inspirada pela obra de Ian Stewart, que nos convida a mergulhar no reino das ciências exatas, onde a matemática encontra a beleza da natureza, oferecendo uma visão única do nosso mundo e de como ele se manifesta em sua forma mais intricada.

Fractais: A Geometria da Natureza
De tempos em tempos, surgem novos campos na matemática. Nos últimos anos, um dos mais notáveis tem sido a geometria fractal, que foi pioneiramente explorada por Benoît Mandelbrot, o criador do termo “fractal” em 1975.
Em linhas gerais, a geometria fractal é um método matemático voltado para a compreensão das aparentes irregularidades presentes na natureza, desvendando suas estruturas ocultas. Este conceito é mais notório por suas imagens geradas por computador, que são ao mesmo tempo complexas e visualmente atraentes, mas seu significado transcende a superfície.
As formas convencionais da geometria euclidiana, como triângulos, quadrados, circunferências e cones, são simples e desprovidas de detalhes particulares. Por exemplo, se ampliarmos uma circunferência, qualquer parte dela se assemelhará cada vez mais a uma linha reta, sem características distintivas notáveis. Essas formas tradicionais desempenharam um papel central na ciência, pois, em muitos casos, sua simplicidade era adequada.
Entretanto, muitas formas na natureza são consideravelmente mais complexas. Árvores possuem uma rede intricada de galhos, nuvens apresentam padrões difusos e sinuosos, montanhas têm contornos irregulares, e os litorais são caracterizados por sua sinuosidade.
Um exemplo interessante são justamente os litorais. Eles exibem curvas sinuosas, mas não podem ser adequadamente descritos por curvas sinuosas convencionais. O aspecto notável é que, em qualquer escala de visualização no mapa, eles parecem semelhantes. Essa característica é conhecida como “estatisticamente autossimilar”. Independentemente do nível de zoom, as características estatísticas dos litorais, como a proporção de baías de determinado tamanho, permanecem consistentes.
Foi Benoît Mandelbrot quem cunhou o termo “fractal” para descrever qualquer forma que mantenha uma estrutura intrincada, independentemente do grau de ampliação. Embora os fractais não precisem ser estatisticamente autossimilares, essa propriedade torna sua compreensão mais acessível. Os fractais que são exatamente autossimilares são ainda mais fascinantes, e foram essenciais para o desenvolvimento desta área.

Os Fractais na História
Há cerca de um século, matemáticos criaram formas estranhas, não apenas estatisticamente autossimilares, mas exatamente autossimilares. Quando ampliadas corretamente, essas formas parecem idênticas às originais.
Um exemplo famoso é a curva do floco de neve, concebida por Helge von Koch em 1904. Ela pode ser construída a partir de três cópias da curva mostrada na figura abaixo.
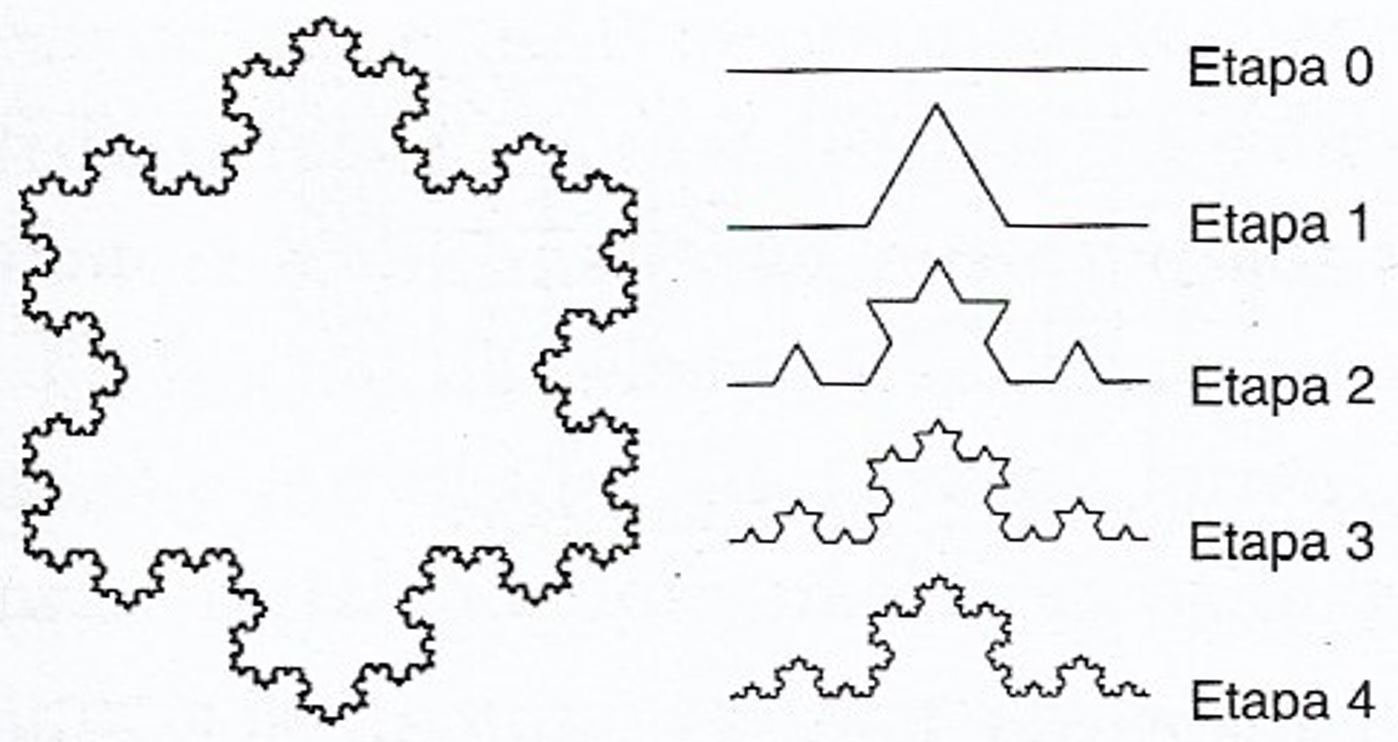
Essa curva componente é exatamente autossimilar (embora o floco de neve como um todo não seja). Podemos ver que cada etapa da construção é formada por 4 cópias da etapa anterior, cada uma com um terço do tamanho. As 4 cópias se encaixam como na Etapa 1.
Passando ao limite infinito, obtemos uma curva infinitamente intrincada construída a partir de 4 cópias de si mesma, cada uma com 1/3 do tamanho – por- tanto, a curva é autossimilar.
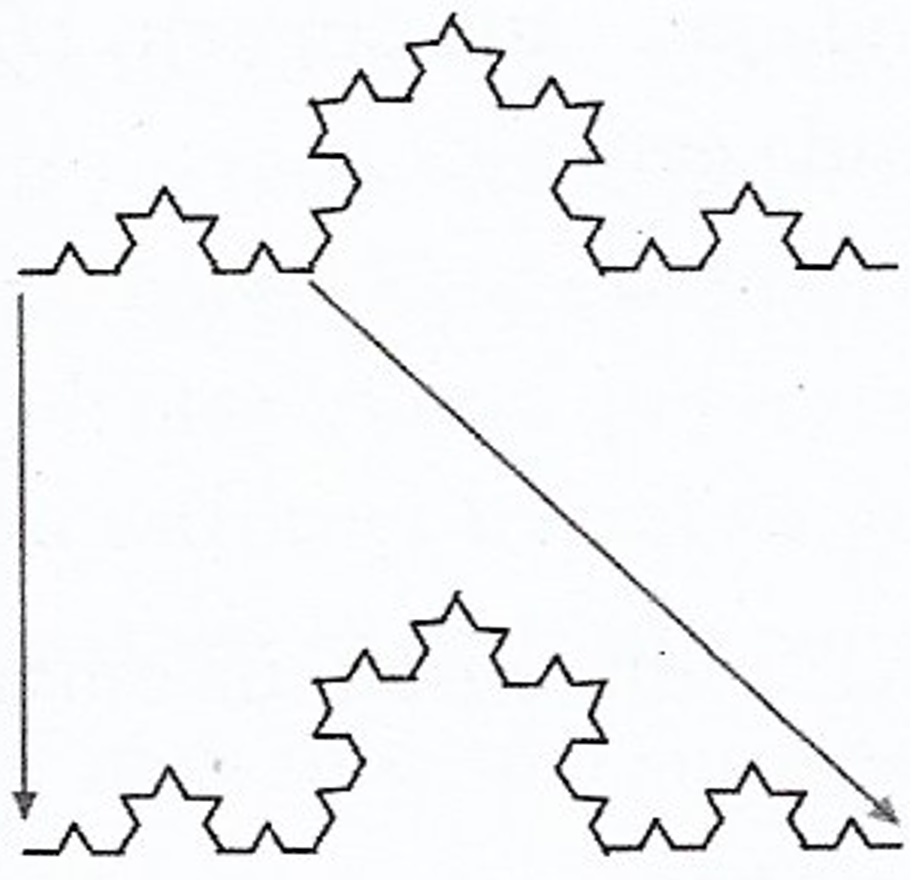
A Dimensão de um Fractal
Embora essa curva seja excessivamente regular para representar um litoral real, a noção de sinuosidade é aproximada, e curvas menos regulares construídas da mesma maneira podem realmente representar litorais. A sinuosidade pode ser quantificada por uma medida conhecida como “dimensão fractal”.
Para mostrar como isso funciona, Ian Stewart no livro “Almanaque das Curiosidades Magnéticas”, pega algumas formas não fractais mais simples e vê como se encaixam em diferentes escalas de ampliação. Ele chama atenção para o fato de que se partir uma reta em pedaços com 1/5 do tamanho, precisará de 5 delas para reconstruir a reta. Com um quadrado, preciso de 25 pedaços, que é 5². E com cubos, preciso de 125, que é 5³.
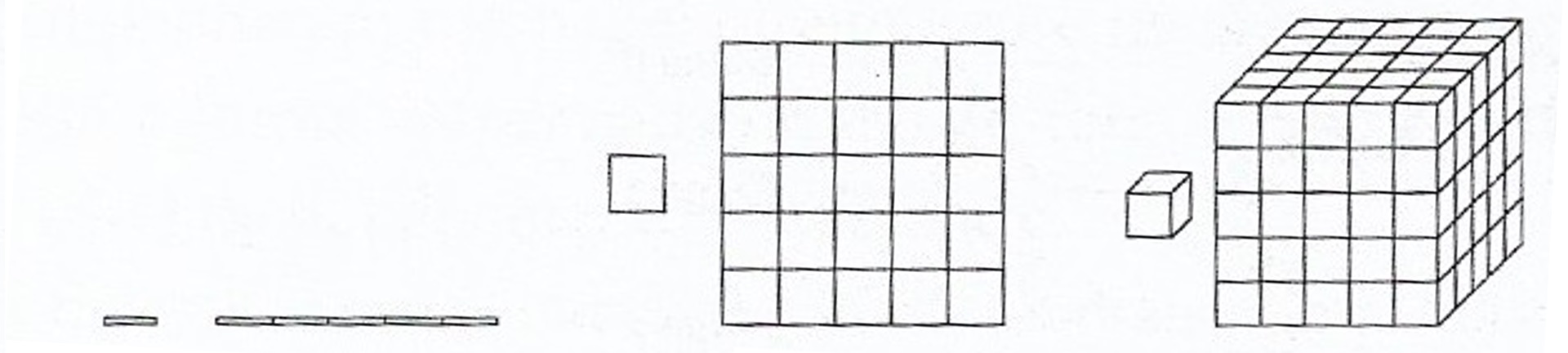
A potência sobre o 5 em cada caso é igual à dimensão da forma em questão: 1 para uma reta, 2 para um quadrado, 3 para um cubo. Em geral, se
queremos encaixar k pedaços de tamanho 1/n de modo a remontar a forma original, então k = n^d . Usando logaritmos, descobrimos que: $$ d = \frac{\text{ln} (k) }{\text{ln} (n) }.$$
Vamos tentar usar esta fórmula no floco de neve. Nesse caso, precisamos de k = 4 pedaços, cada um com 1/3 do tamanho, portanto n = 3. Assim, nossa fórmula gera: $$d = \frac{\text{ln} (4) }{\text{ln} (3) },$$ que é aproximadamente 1,2618. Dessa forma, a “dimensão” da curva do floco de neve não é um número inteiro.
Isso seria ruim se quiséssemos pensar em “dimensões” do modo convencional, como o número de direções independentes disponíveis. Mas está tudo bem se o que quisermos for uma medida numérica da sinuosidade, com base na autossimilaridade. Uma curva com dimensão 1,2618 é mais sinuosa que uma curva de dimensão 1, como uma linha reta; mas é menos sinuosa que uma curva de dimensão 1,5, por exemplo.
Há dezenas de maneiras tecnicamente distintas de definir a dimensão de um fractal. A maior parte delas funciona quando o fractal não é autossimilar. A definição usada pelos matemáticos é chamada dimensão de Hausdorff-Besicovitch. É uma coisa espinhosa de se definir e de se calcular, mas tem propriedades agradáveis. Os físicos geralmente usam uma versão mais simples, chamada box dimension.
Esta é fácil de calcular, mas carece de quase todas as propriedades agradáveis da dimensão de Hausdorff-Besicovitch. Apesar disso, as duas dimensões geralmente são iguais. Portanto, o termo dimensão fractal é usado para se referir a ambas.
Os fractais não precisam ser curvas: podem ser superfícies ou sólidos altamente intrincados, ou também formas de maiores dimensões. A dimensão fractal, portanto, mede a aspereza do fractal, e com que eficiência ele preenche o espaço. A dimensão fractal surge na maioria das aplicações dessas figuras, tanto em cálculos teóricos como em testes experimentais. Por exemplo, a dimensão fractal dos litorais reais geralmente se aproxima de 1,25 – surpreendentemente próxima à da curva do floco de neve.
Aplicações dos Fractais
Os fractais têm uma ampla gama de aplicações, que vão desde a análise detalhada de minerais até a compreensão da estrutura do universo. Na engenharia, os fractais são usados para projetar antenas de telefonia celular mais eficientes, e técnicas fractais de compressão de imagens permitem armazenar grandes volumes de dados em CDs e DVDs.
Na medicina, a geometria fractal pode ser usada para identificar células cancerosas, que tendem a apresentar superfícies enrugadas com uma dimensão fractal superior à das células normais.
Recentemente, um grupo de biólogos descobriu que a geometria fractal pode explicar padrões em seres vivos que anteriormente eram um mistério. Esses padrões estão relacionados a “leis de escala” estatísticas, como a relação entre as taxas metabólicas de animais e suas massas corporais.
A geometria fractal oferece uma explicação elegante para essas relações, considerando a rede ramificada de veias e artérias responsável pelo transporte de líquidos, como o sangue, nos organismos.
Em suma, os fractais evoluíram consideravelmente e são agora amplamente utilizados como modelos matemáticos em diversas áreas da ciência. Além disso, são a base de eficazes métodos de compressão de vídeo digital.
Apoie Nosso Trabalho:
Apoie nosso trabalho fazendo um pix de qualquer valor: Chave Pix: 06713646697
Mais intrigante ainda é o fato de que os fractais representam a geometria subjacente de muitas formas naturais. Por exemplo, o brócolis romanesco exibe a mesma estrutura fractal em cada uma de suas flores, organizadas em espirais de Fibonacci em escalas cada vez menores. Isso ilustra como a geometria fractal está intimamente relacionada ao crescimento das plantas, o que, por sua vez, é influenciado por sua genética. Nesse contexto, a geometria não é apenas uma curiosidade visual, mas desempenha um papel fundamental.

Conclusão
À medida que concluímos nossa exploração pelo enigmático universo dos fractais, podemos perceber o quão profundamente essa disciplina matemática transformou nossa compreensão da natureza e do mundo que nos cerca.
Inspirados pelo livro “Almanaque das Curiosidades Matemáticas” de Ian Stewart, pudemos desvendar os segredos por trás das formas complexas e aparentemente caóticas presentes em nossa realidade.
Os fractais não são apenas uma expressão da beleza matemática; eles representam uma ponte entre a matemática pura e as aplicações práticas em campos tão diversos como a engenharia, a medicina e a ciência da computação.
Nossa jornada nos mostrou como essas estruturas intrincadas são a base para resolver uma miríade de desafios do mundo real, desde o design de antenas mais eficientes até a identificação de células cancerosas.
À medida que continuamos a explorar esse fascinante reino, lembramo-nos de que a matemática, muitas vezes vista como uma disciplina árida e abstrata, pode, na verdade, ser uma ferramenta poderosa para decifrar a complexidade da natureza.
Os fractais são um testemunho da profunda conexão entre a matemática e o mundo que nos rodeia, revelando a beleza intrínseca da geometria da natureza.

Leia Mais:
- A Ordem No Caos: A História do Efeito Borboleta de Lorenz
- Como Aprender Matemática Sozinho? As Melhores Técnicas de Estudo
- Arquimedes: Como as ideias deste matemático criaram Shrek, Avatar e Toy Story?
- A beleza da matemática na Razão Áurea (ou Número de Ouro)
PRECISANDO DE AJUDA COM SEUS EXERCÍCIOS SOBRE ESTE CONTEÚDO? Entre em contato com a gente via WhatsApp clicando aqui. |
